Outils pour utilisateurs
Ceci est une ancienne révision du document !
Table des matières
Algorithmes sur les graphes
Il existe 2 méthodes pour parcourir un graphe :
•Le parcours en largeur
•le parcours en profondeur
•Chercher une chaine dans un graphe
A quoi ça sert ?
Les parcours d'algorithmes permettent de voir les liens entre eux entre différents éléments. L'idée du “parcours” est de “visiter” tous les sommets d'un graphe en partant d'un sommet quelconque.
Le parcours en largeur
VARIABLE
G : un graphe
s : noeud (origine)
u : noeud
v : noeud
f : file (initialement vide)
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
s.couleur ← noir
enfiler (s,f)
tant que f non vide :
u ← defiler(f)
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
v.couleur ← noir
enfiler(v,f)
fin si
fin pour
fin tant que
FIN
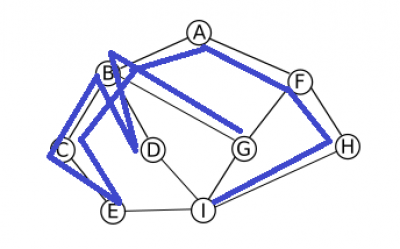
Voyez ce programme comme une tache d'encre qui s'étend.
Le programme va d'abord visiter les taches adjacentes au point de départ pour visiter ceux de plus en plus loin.
Si on part du point I on aura un ordre de visite de: I , E , H , C , D , G , H , B , F et A
La distance entre le point I et celui visité est indiqué sur le graphe ci dessous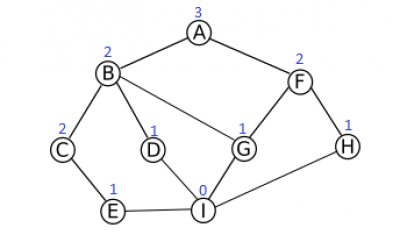
Le parcours en profondeur
Dans le cas du parcours en profondeur, on va chercher à aller “le plus loin possible”.
La méthode de découverte est unidirectionnelle.
VARIABLE
G : un graphe
u : noeud
v : noeud
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
PARCOURS-PROFONDEUR(G,u) :
u.couleur ← noir
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
PARCOURS-PROFONDEUR(G,v)
fin si
fin pour
FIN
Cycle dans les graphes
Qu'est qu'un cycle ?
Un cycle est tout simplement une boucle dans un graphe, c'est utile pour savoir s'il est possible d'effectuer un parcours qui revient à son point de départ sans être obligé de faire demi-tour.
L'algorithme ci dessous permet de “détecter” la présence d'au moins un cycle dans un graphe.
VARIABLE
s : noeud (noeud quelconque)
G : un graphe
u : noeud
v : noeud
p : pile (vide au départ)
//On part du principe que pour tout sommet u du graphe G, u.couleur = blanc à l'origine
DEBUT
CYCLE():
piler(s,p)
tant que p n'est pas vide :
u ← depiler(p)
pour chaque sommet v adjacent au sommet u :
si v.couleur n'est pas noir :
piler(v,p)
fin si
fin pour
si u est noir :
renvoie Vrai
sinon :
u.couleur ← noir
fin si
fin tant que
renvoie Faux
FIN
Chercher une chaine dans un graphe
Ici nous cherchons à connaitre le chemin entre deux noeuds
![]() cet algorithme renvoie un chemin, ce n'est pas forcement le plus court
cet algorithme renvoie un chemin, ce n'est pas forcement le plus court
VARIABLE
G : un graphe
start : noeud (noeud de départ)
end : noeud (noeud d'arrivé)
u : noeud
chaine : ensemble de noeuds (initialement vide)
DEBUT
TROUVE-CHAINE(G, start, end, chaine):
chaine = chaine ⋃ start //le symbol ⋃ signifie union, il permet d'ajouter le noeud start à l'ensemble chaine
si start est identique à end :
renvoie chaine
fin si
pour chaque sommet u adjacent au sommet start :
si u n'appartient pas à chaine :
nchemin = TROUVE-CHAINE(G, u, end, chaine)
si nchemin non vide :
renvoie nchemin
fin si
fin si
fin pour
renvoie NIL
FIN